Estimating Distance and Direction Traveled
The wayfinder uses a dead reckoning system in to determine his course. He knows his starting point and the distance and direction to his destination. He develops a course strategy and draws an imaginary reference course (based on average conditions) to his destination. As he estimates his direction and distance traveled each day, he mentally plots his position against this reference course to his destination and estimates how many more days it will take him to reach his destination.
He sets the direction in which the canoe is heading by celestial bodies and ocean swells, and subtracts leeway; he estimates his distance traveled by multiplying his estimated speed by the time lapsed since his last position determination.
An experienced wayfinder can estimate speed by watching the motion of the water as it passes the canoe.

An inexperienced wayfinder can determine the speed of the canoe by timing marks (bubbles or objects in the water) moving past two points on the canoe. On Hokule'a, the wayfinder times bubbles moving between the front and back 'iako (crossbeams joining the two hulls together), a distance of 42.2 feet.
The approximate speed in knots for various time intervals of objects passing Hokule'a can be memorized in the following table:
3 seconds - 8.5 knots
4 seconds- 6.5 knots
5 seconds- 5 knots
6 seconds- 4 knots
7 seconds- 3.5 knots
8 seconds- 3 knots
10 seconds- 2.5 knots
12 seconds- 2 knots
15 seconds- 1.5 knots
25 seconds- 1 knot
An estimate of speed can be gotten by dividing 25 by the number of seconds it takes the object to travel 42.2 feet: e.g. 25 divided by 3 seconds = 8.33 knots, rounded up to 8.5 knots.
The formula is nautical miles per hour = distance, converted to nautical miles, divided by time, converted to hours: 42.2 feet = .007 nautical miles (42.2 divided by 6077 feet in a nautical mile); 3 seconds = .0008 hours (3 divided by 3600 seconds per hour); nautical miles per hour equals .007 divided by .0008, or 8.75 knots.
Time during the day can be estimated by the position of celestial bodies; twenty-four hours from sunrise to sunrise; around twelve hours from sunrise to sunset; around six hours from sunrise till noon; and so on. The sun, moon, or stars travel at about one degrees every four minutes, taking about three hours to get 45 degrees on the celestial sphere.
Knowing direction, speed, and time elapsed, the wayfinder can estimate the course and distance made good per day. The calculations can become quite complex if the canoe changes direction during the day, or when wind speed varies; the calculation for the day is then the sum of various separate calculations. To simplify calculations and to monitor his food and water supplies, the wayfinder may use sailing days rather than miles to keep track of how far is from his departure point and how far his destination is.
One sailing day for Hokule'a equals about 120 miles in the trade wind zones where winds average 10-20 knots; two sailing days from Hawai'i equal 240 miles.
Compensating for Leeway in the Canoe’s Heading
When a canoe is sailing with the wind forward of its beam, its actual heading is not the same as its apparent heading because it is being pushed off its course by the wind. The angle between the apparent heading of the canoe and the direction the canoe is actually traveling through the water is referred to as leeway. This angle may vary from 4-15 degrees to leeward, depending on (1) the strength of the wind; (2) the angle the canoe is sailing into the wind (the greater the angle, the greater the leeway); (3) the draft of the canoe (deep-keeled boats have a smaller leeway than shallow-keeled boats); (4) the speed of the canoe (the greater the speed, the less the leeway).
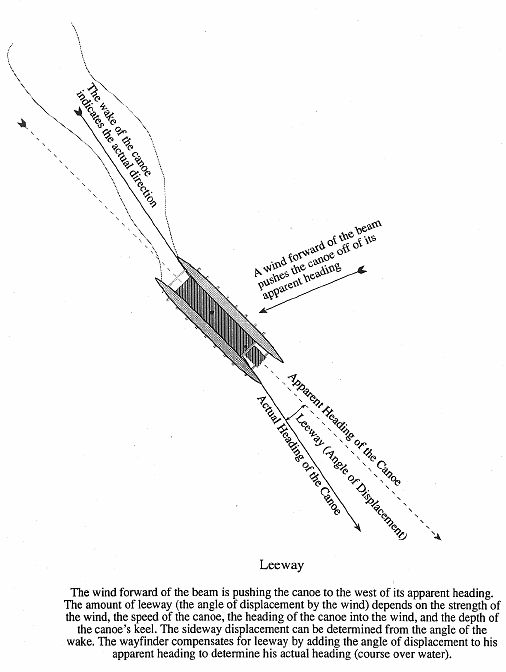
The wayfinder must compensate for leeway by pointing the canoe more sharply into the wind, or if the canoe is pointed as far as possible into the wind as it can go, he subtracts leeway to determine his course made good, or actual heading. For example, when the wayfinder wants to go in the direction of Manu Malanai (SE) and the wind and current is pushing the canoe one house further south (toward Nalani Malanai, or SE by S), the wayfinder must point the canoe one house further north (toward Noio Malanai or SE by E) to make good his direction of Manu Malanai; if he cannot point the canoe any farther into the wind, then his course made good is actually Nalani Malanai (SE by S), rather than its heading of Manu Malanai (SE).
The wayfinder can calculate the amount of leeway he must compensate for in his heading by observing the wake of the canoe in relationship to the direction of the canoe. The angle between the direction of the canoe and the wake behind the canoe tells the wayfinder how much sideways displacement there is due to the wind. Another method, if it is practical, would be to attach a line near the center of the sail effort of the canoe and to calculate the angle of this line from the centerline of the canoe. An experienced wayfinder, knowing well the capabilities of his canoe, will be able to estimate leeway given the direction of his heading and the speed of the wind working against the canoe.
